问题分诊室
基于GBRT模型的海洋平台结构裂纹扩展识别
发布时间: 2024-09-03
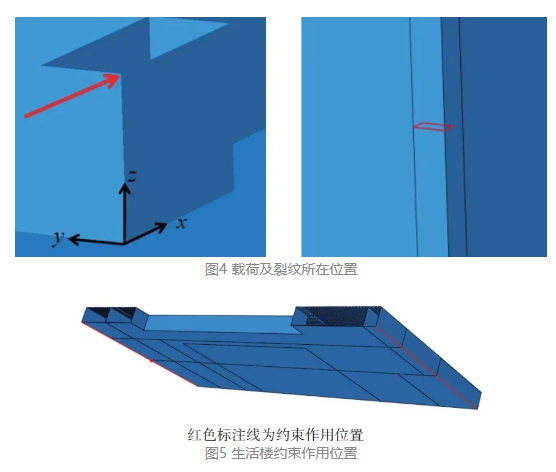
某海洋平台在多次维修中发现在生活楼与甲板连接的角隅处的裂纹有扩展现象,提出了根据裂纹周边多维应变进行裂纹长度识别的思想。搭建了含有初始裂纹的海洋平台有限元模型,以多维应变数据和对应裂纹长度分别作为机器学习模型特征输入与输出,通过梯度回归提升树(GBRT)模型对裂纹长度进行预测。测试结果表明,该模型对裂纹长度预测MSE(均方误差)值可达0.0006,R2可达0.9991,且该模型对噪声有良好的抗干扰性。
20世纪以来,中国海域内大量的海洋平台建成并投入使用,其中多数平台已超出使用年限,存在严重安全隐患。平台的超期服役和恶劣的工作环境所导致的裂纹损伤带来了严重安全问题,如结构强度承载力下降,连接位置海水渗漏,更严重会使平台结构整体失效。以“南海挑战号”FPSO(浮式生产储卸油装置)为例,该平台1975年在加拿大建造,1995年完成改造,2007年上半年在油田现场进行了局部大修,2010年入坞大修。平台入坞后发现一系列结构安全问题,包括:腐蚀问题,如平台结构、管线腐蚀严重,检测到的减薄点最大减薄率达到70%、平台桩腿海水飞溅区腐蚀严重,局部坑蚀超标、系泊系统平台链腐蚀超标;裂纹问题,水下结构存在裂纹需做修复,平台主结构多处存在裂纹。2012年对另一座在役半潜式钻井平台进行了无损探伤检测,也发现缺陷多达37处,其中有3处渗漏。平台结构构件存在裂纹等结构损伤,会严重威胁平台结构安全。
随着光纤传感技术的广泛应用,科研人员对光纤传感器在裂纹监测领域进行了初步研究。Yang等研发了一种塑性增强的光纤传感器,通过分析其高频信号能有效监测疲劳荷载作用下裂纹的产生和扩展。Jin等对具有孔边裂纹的铝合金板的裂纹扩展进行了监测,对裂纹扩展时光纤光栅传感器(fiber grating sensor,FBG)的反射光谱特性进行了研究。何弯弯等通过在空间柔性结构表面布设光纤传感器网络,建立了光纤传感器应变响应值与裂纹长度的关系模型,实现了裂纹的损伤识别与定位。方桂华运用FBG传感器阵列对悬臂梁在简谐振动下的应变阵列数据进行分析,以应变功率谱频响函数作为裂纹损伤的识别指标。黄博等通过FBG应变传感器数据将动态应变响应作为损伤识别指标,实现了金属裂纹的识别定位。Gao等将光纤直接粘贴到混凝土桩的表面,通过光频域反射计(OFDR)技术来监测混凝土桩在连续变化的荷载下的应变情况。Sounthararajah等运用OFDR技术监测水泥路面梁在静态和动态荷载下的弯曲应变,能有效地发现梁上裂纹的产生及扩展。
近年来,随着人工智能的发展,人们逐渐开发出了利用机器学习及深度学习的裂纹识别方法。Li等提出一种k-means算法,该模型可以更好地完成航空发动机部件的表面缺陷检测任务。Su等利用改进的语义分割方法实现了海洋平台裂纹的识别,通过像素级的方式将裂纹区域描绘出来。Jia等通过多种改进的目标检测方法,对海上浮式生产储卸油装置的支墩裂纹进行识别。
针对传统裂纹监测方法的不足,提出了基于多尺度应变结合机器学习进行裂纹扩展预测的方法。在简介裂纹监测的研究背景的基础上,用有限元方法对海洋平台结构裂纹的扩展过程进行模拟,并提取了裂纹周边应变特征。根据梯度回归提升树(GBRT)模型的广泛应用,利用GBRT模型进行训练。最后,将部分多尺度应变作为测试集对训练得到的优化模型进行验证。
裂纹扩展的多尺度应变提取
1.1 基于扩展有限单元法的裂纹扩展模拟方法
扩展有限单元法(extended finite element method,XFEM)是由美国西北大学教授Belytschko为代表的研究组于1999年提出的一种求解不连续力学问题的数值方法。通过在常规有限元方法基础上,加入局部增强函数以增加裂尖单元的自由度,来实现裂纹的扩展模拟。
扩展有限单元法计算含裂纹区域节点位移u包括节点的连续位移uc和不连续位移udisc2部分
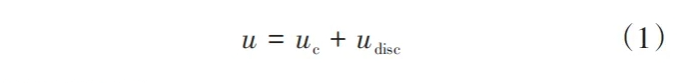
节点的连续位移表示为

式中,Ns为离散区域的节点集,Ni为节点的形函数,ui为节点位移。
在图1中,对于裂纹完全贯穿的单元,不连续位移可以表示为
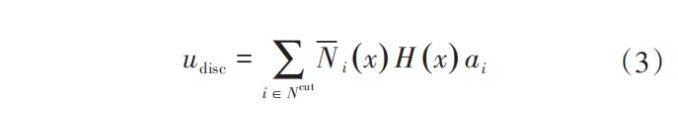
式中,Ncut为完全被裂纹切割的节点集,H(x)为广义阶跃函数,在裂纹上侧等于1,下侧等于−1。
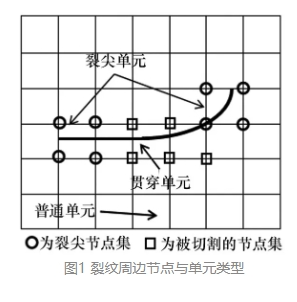
含裂尖的单元节点的不连续位移表示为
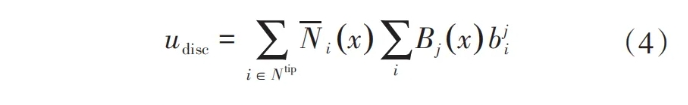
式中,Ntip为裂尖节点集,Bj(x)为裂尖加强函数,表示为

将式(2)~(5)带入式(1)可得裂纹区域节点位移函数



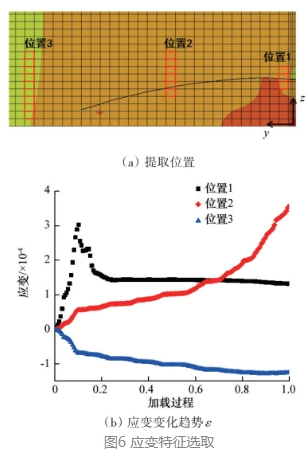
根据有限元应变变化过程,在裂纹周边选取20个应变传感器安装位置。如图7所示,分布式光纤应变传感器测量范围分别为30、60、90mm,由此实现对裂纹周边影响区域的多尺度应变信息采集。
裂纹长度识别算法的基本思想
GBRT算法是一个回归模型,主要用于拟合数值,是一种集成学习算法。提升树主要采用加法模型,主要思想是不断拟合残差,利用梯度下降法拟合残差。GBRT算法是一种迭代的回归树算法,由多棵回归树组成,所有回归树的结论累加起来为最终结果。GBRT算法使用了前向分布算法,其思想是基于当前模型和拟合函数选择合适的决策树函数,从而最小化损失函数。
GBRT的加法模型如下

其算法流程为,
Step1:准备训练数据集T=(x1, y1),(x2,y2),…,(xN,yN)
Step2:初始化f (0)(x)
Step3:for t=1 to T do

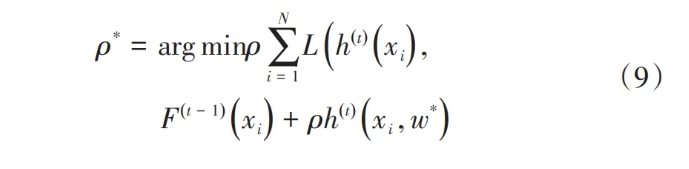
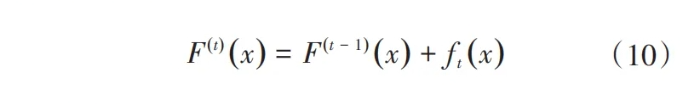
Step4:输出F(t)(x)
2.2 网格搜索
网格搜索用于选取模型的最优超参数。在超参数和目标指标之间的关系比较复杂或者无法显示表达时,需要去尝试不同的超参数的取值,最终选择结果较好的超参数取值。网格搜索通过循环遍历每个自由超参数的每一种组合得到对应的模型,从而筛选出最佳参数的组合。
基于GBRT算法的裂纹扩展长度识别
在有限元模拟中,裂纹扩展增量大小受到网格尺寸和载荷大小的限制;但在实际扩展过程中,裂纹扩展过程中裂纹长度变化是连续的。为了实现裂纹长度的连续预测,需要将有限元模拟结果带来的裂纹扩展长度识别问题转化为多元非线性回归问题。
3.1 训练集在总样本中占比的影响
平台裂纹扩展过程受实际工况的影响可能与模拟结果有所不同,且实际的监测数据难以获取。因此,将有限元模拟得到的一部分样本作为训练集进行模型训练,利用该模型对其他样本进行预测,来验证回归模型的适用性。
以上述20个应变传感器提取的多尺度应变数据作为输入变量数据,以裂纹长度的变化作为输出。在本次模拟实验结果中,分析步数量为158步;即该模型样本总数N=158,每个样本所包含的特征数为20。同时为避免数据特征尺度不同和异常值导致模型准确度下降,需要将原始数据进行归一化处理。
将总的样本N随机分为训练集N1和测试集N2,在经典的机器学习理论下训练集占总样本比例为25%,测试集占总样本比例为75%。在图8中,横轴为样本裂纹长度的真实值,纵轴为模型的预测值。可以看出训练集与预测集分布较为一致。
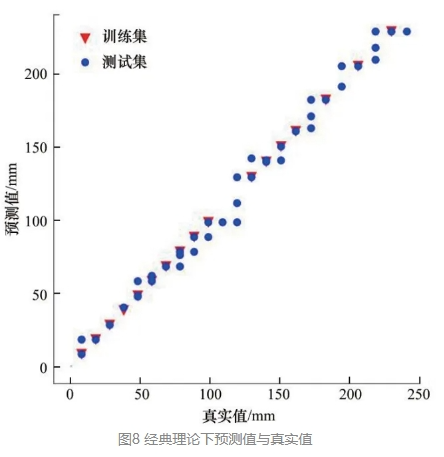
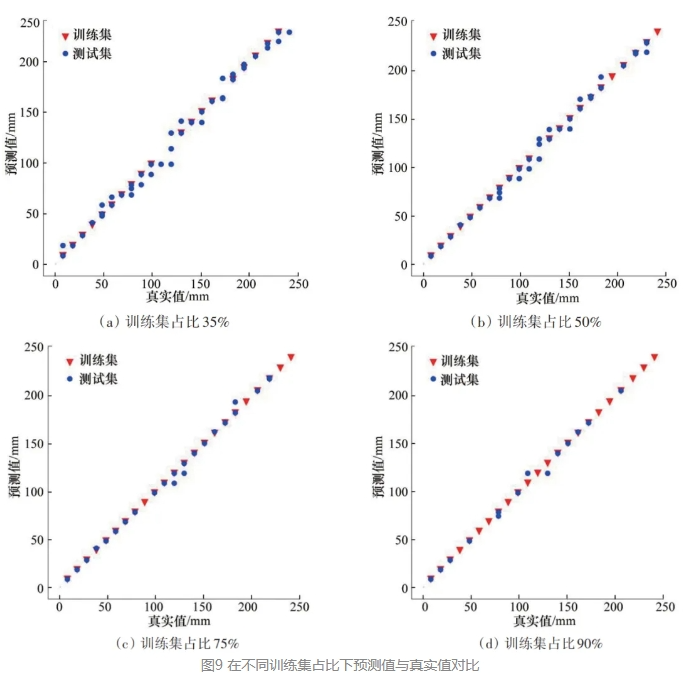
逐步提高训练集样本数在总样本数中的占比,以期提高机器学习水平。因此,将训练集样本比例提高至35%、50%、75%和90%。同时可以验证不同数据集对整体训练结果带来的影响,结果如图9所示。
3.2 网格搜索寻找最优参数
涉及的模型评价指标为均方误差(MSE)和R2。
1)MSE用于衡量平均误差,可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
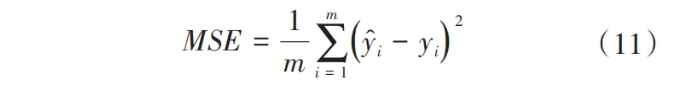
2)R2是机器学习中判断模型拟合程度好坏的指标,R2越接近1,表示模型拟合效果越好。
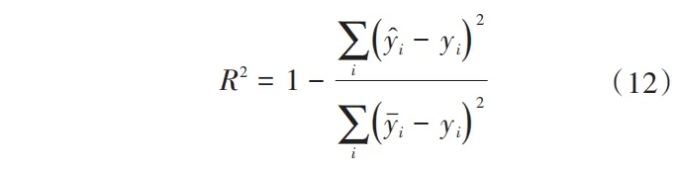
根据表1范围,对模型超参数进行网格搜索。在n_estimators为500、learning_rate为0.01、max_depth为4、min_samples_split为2的情况下预测结果最优。
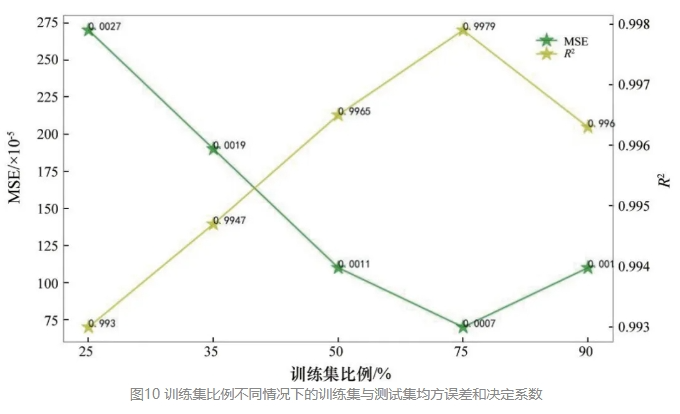
图10给出了测试集与训练集在上述比例下模型的均方误差和R2。在初始阶段,训练集占比逐渐增大时,测试集均方误差逐步下降且R2逐渐上升,代表模型学习到的信息更多。此过程表明,在训练过程中,模型的参数更加贴近真实的数据情况。在训练集比例达到75%之前,该模型的学习程度不断加深,各参数的更新更符合裂纹的扩展情况。当训练集的比例到达90%时,均方误差上升且R2下降,意味着训练集过多而测试集过少,训练集和测试集的分布比例相差过大会导致均方根误差增加,即在这种情况下的误差相比训练集比例达到75%时的误差更大。同样地,其R2也出现了下降的问题,2个指标可以表明模型出现过拟合现象。后续部分以训练集比例75%为前提进行分析与训练。
3.3 重要输入特征重要性排序
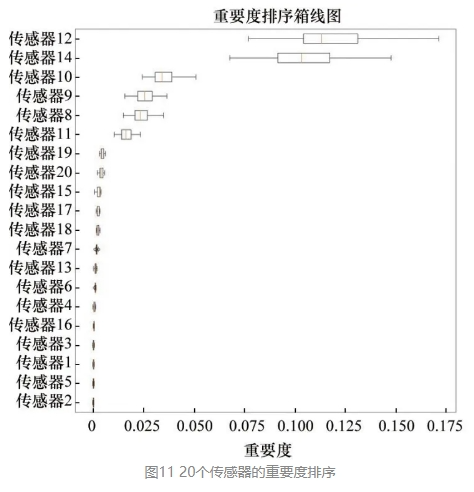
建立模型之后,特征重要性能够增强模型的可解释性,帮助建立对应于应力点与裂纹长度识别的依赖关系模型。同时为了避免不重要特征的输入引起的对模型的干扰,以及便于冗余信息的排除,提高模型的训练速度,对20个传感器的重要度进行分析。基于置换检验的思想对特征重要性进行检测,模型训练完成后,通过模型的Permutation_Importance功能查看输入特征对预测长度的影响。
根据图11所示,传感器12、14、10、9、8、11所收集的应力数据对最后裂纹长度的影响较为显著,可以看出距离裂纹位置较近的应力变化对模型的影响非常小,对于竖直排列的传感器位置的应力数值为裂纹预测的主导特征。可以看出,应力数值的分布范围越大,变化越明显,其特征的重要性越高。经过验证,只输入传感器12、14、10、9、8、11的应力数据得到的均方根误差为0.9979,R2为0.0007,与上文中输入20个特征的结果相同,同时验证了其余传感器的信息多为冗余信息,可以剔除这些特征从而提高运算效率。
3.4 噪声对SVR(支持向量回归)模型的影响
在实际监测中环境噪声和系统噪声等都会对模型预测准确率产生影响,有必要对不同噪声水平下的模型误差进行对比。通过对全部样本添加5%、15%、30%、50%的噪声水平,观察GBRT模型对噪声的抵抗能力来验证模型的鲁棒性。如图12所示,分别为添加5%、15%、30%、50%噪声水平时,所有样本下裂纹长度的真实值与预测值的对比。
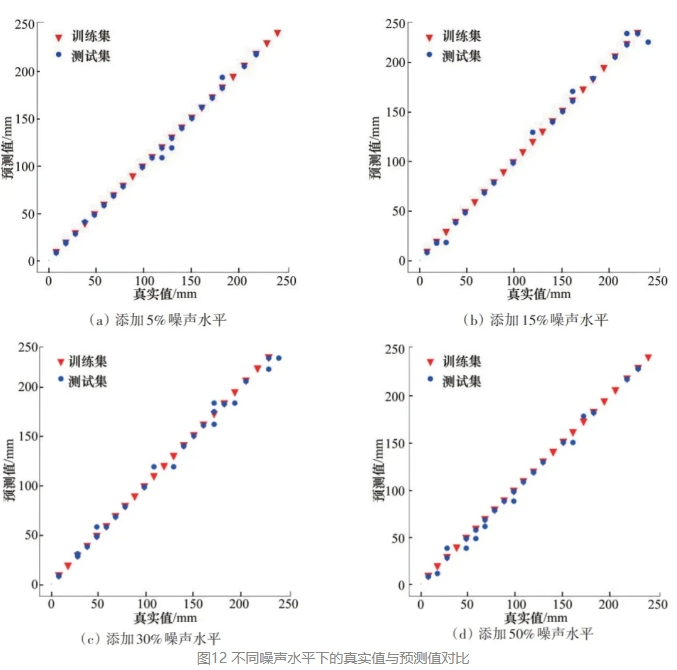
由表2可以看出,在5%、15%、30%、50%噪声水平下,最大均方根误差为0.0017,R2为0.9956,表明了GBRT模型具有良好的鲁棒性,在50%噪声影响下仍能对裂纹长度做出相当准确的预测。
结论
从海洋平台生活楼处的裂纹损伤监测问题出发,提出了利用多尺度光纤应变结合机器学习方法进行裂纹监测的解决方案。利用GBRT模型建立多尺度应变数据与裂纹扩展长度的映射关系,经研究获得如下结论。
在不改变海洋平台主体结构的基础上,对生活楼4个角处制定了3种加固方案。通过常规有限元分析方法,最终的加固方案可以有效降低生活楼4个角隅部在受到风力及波浪荷载作用时的最大主应力。
为实现生活楼局部模型的裂纹扩展试验过程,利用XFEM方法在海洋平台生活楼右后角隅部加入初始长度的一定的初始裂纹。在水平荷载下最终加固方案可以抑制裂纹的扩展。裂纹附近应变呈梯度分布。
通过GBRT算法预测结果与真实值吻合良好,MSE为0.0006,R2为0.9991。通过对该模型加入高斯噪声,模型最低结果MSE为0.0017,R2为0.9956,结果表明,该裂纹监测方法可适用于相关监测范围,对工程中的安全监测问题产生支持或参考的作用。
本文作者:李阳、苏馨、代彤彤、张崎、黄一、贾子光
作者简介:李阳,大连理工大学船舶工程学院,中国海洋石油集团有限公司,高级工程师,研究方向为海洋工程结构;贾子光(通信作者),大连理工大学化工海洋与生命学院,副教授,研究方向为海洋平台结构安全。